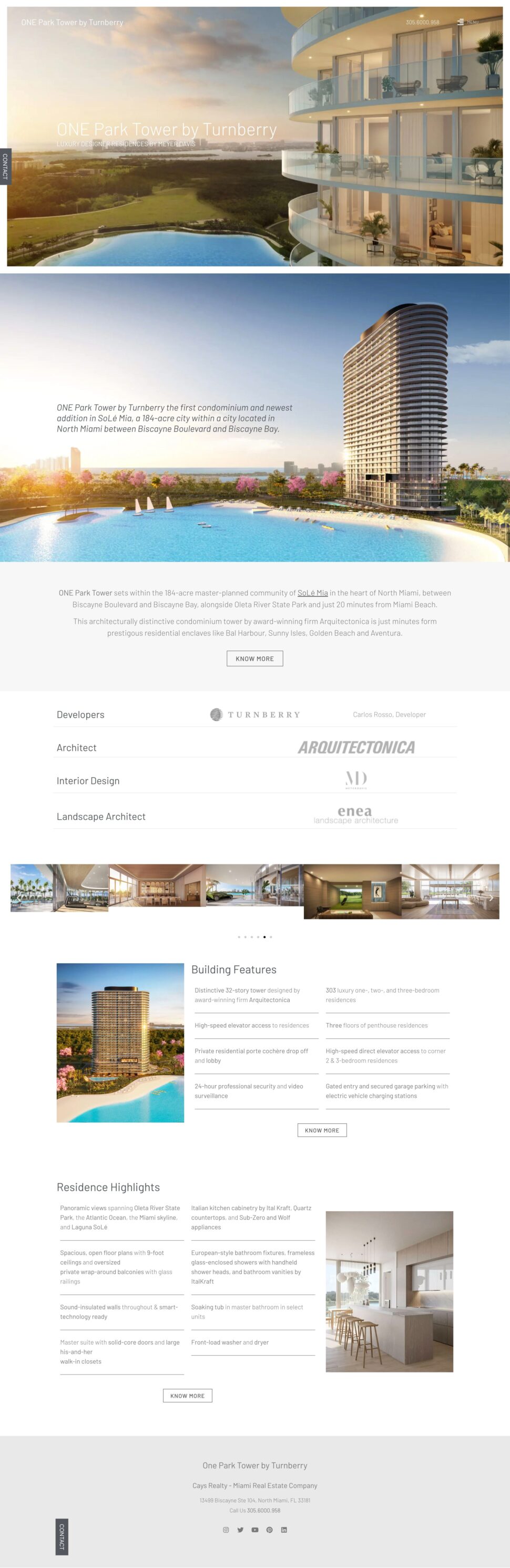
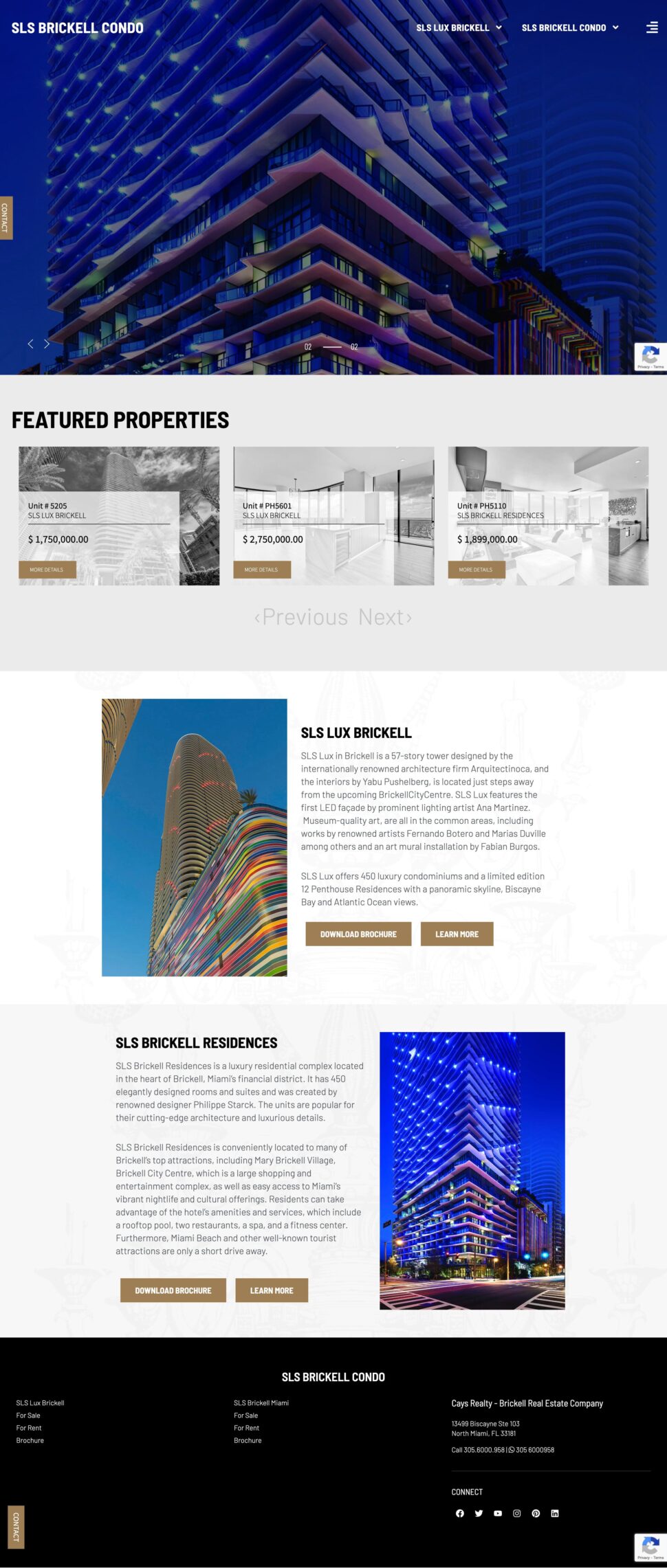
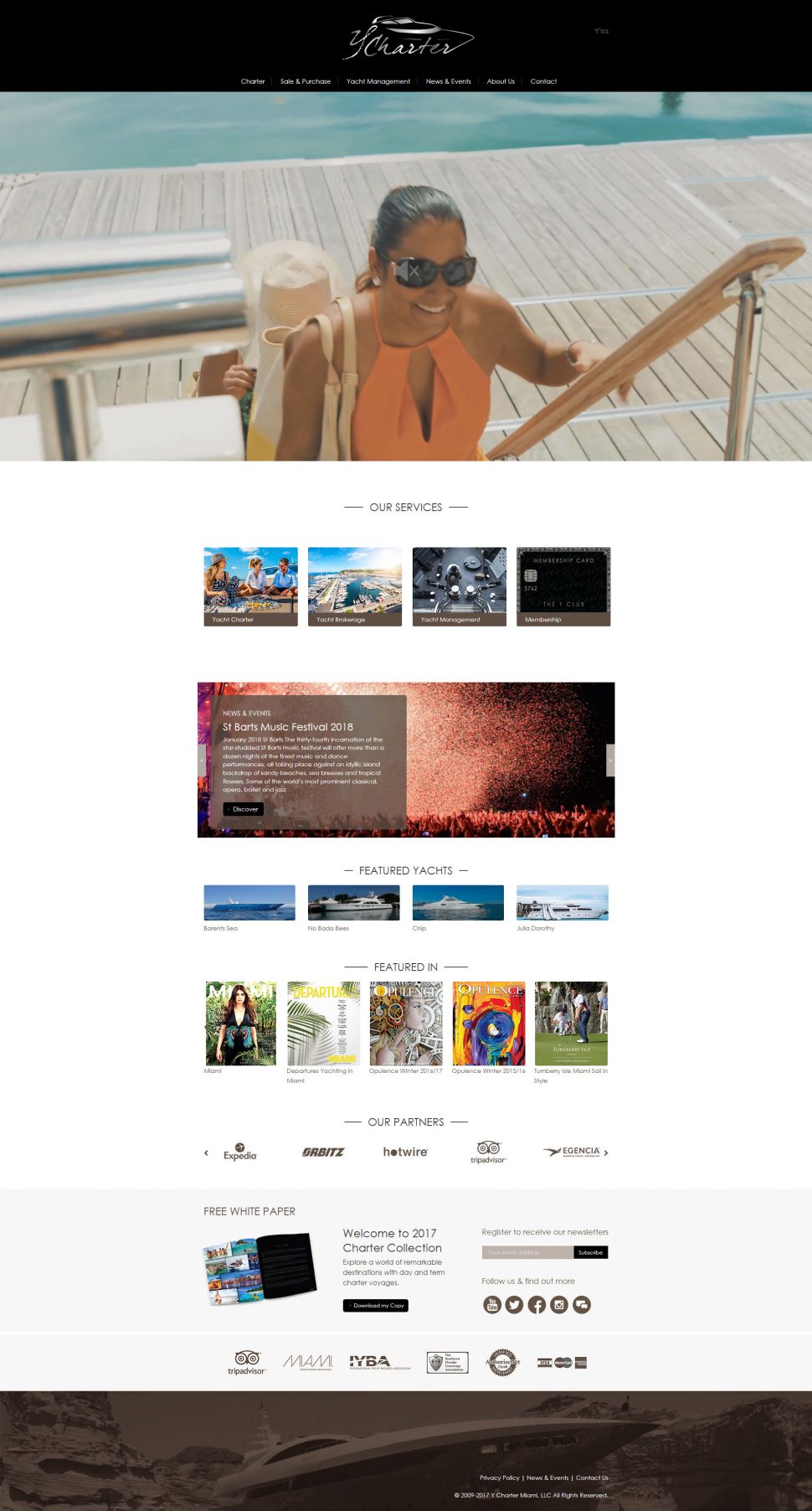
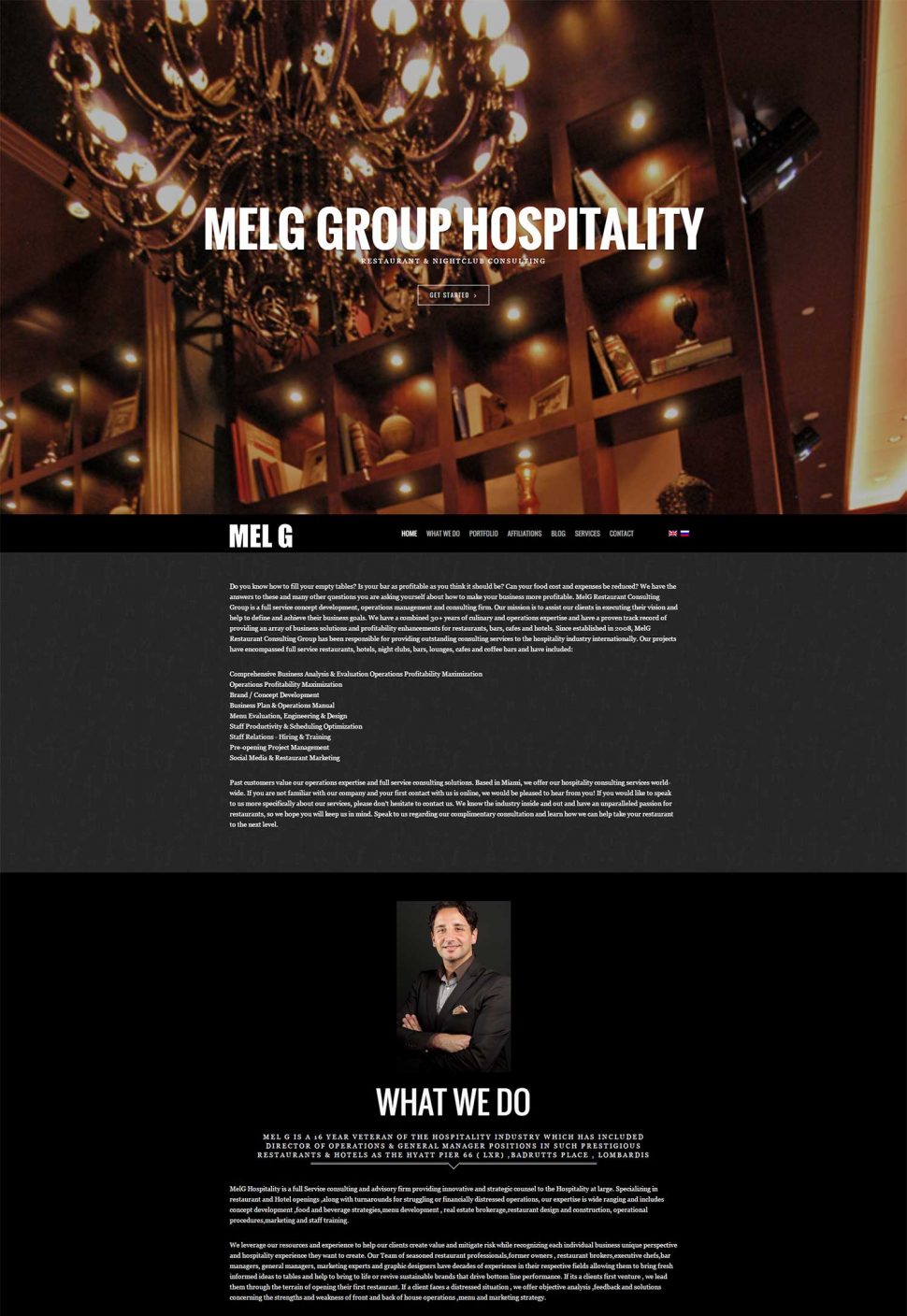
Dominor is a Web design and Internet Strategy Company that has been providing clients with online interactive solutions and consulting services for more than a decade. We highlight the increasing demand for streamlined Information Technology services across various types of setups and startups. Our aim is to provide clients with robust and expert solutions that will exceed the objectives of their business.
We employ highly-effective strategies and forward-looking personnel to handle the needs of our clients for superior quality IT solutions. With services ranging from backend infrastructures with user-friendly environment to large-scale Internet marketing and custom application development, we are ready to provide solution to a diverse range of online ventures.
Projects that land on our desk are managed efficiently with expert attention to detail and optimum dedication. Through efficient strategies, techniques and integration of client-side objectives, our services aim to produce quality results, exceeding expectations. And our years in the industry have helped us understand a variety of markets, prompting us to continuously evolve and adapt to a spectrum of changes and innovations.